Multi model comparison

We often want to compare the result of multiple models.

Calibration. We have several “runs” of the same model with different settings. We would like to find the best.

Validation. We would like to compare our model with alternative models, e.g. a regional DHI model or an external model.

In this notebook, we will consider several wave models for the Southern North Sea and compare to both point measurements and satellite altimetry data.

import numpy as np
import modelskill as ms

Define observations

o1 = ms.PointObservation('data/SW/HKNA_Hm0.dfs0', item=0, x=4.2420, y=52.6887, name="HKNA")
o2 = ms.PointObservation("data/SW/eur_Hm0.dfs0", item=0, x=3.2760, y=51.9990, name="EPL")
o3 = ms.TrackObservation("data/SW/Alti_c2_Dutch.dfs0", item=3, name="c2")

Define models

mr1 = ms.model_result('data/SW/HKZN_local_2017_DutchCoast.dfsu', name='SW_1', item=0)
mr2 = ms.model_result('data/SW/HKZN_local_2017_DutchCoast_v2.dfsu', name='SW_2', item=0)
mr3 = ms.model_result('data/SW/ERA5_DutchCoast.nc', name='ERA5', item="swh")

##

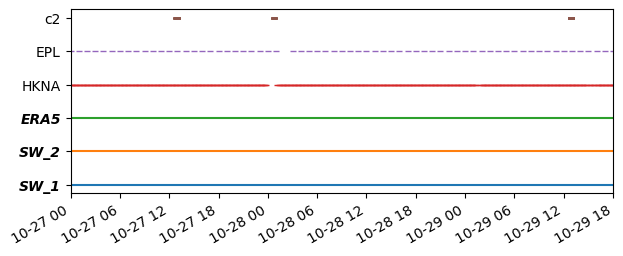
Temporal coverage

ms.plotting.temporal_coverage([o1, o2, o3], [mr1, mr2, mr3]);

Match observations and model results

# HKNA is outside ERA5 domain -> pick nearest grid cell
cc = ms.match(obs=[o1, o2, o3], mod=[mr1, mr2, mr3], spatial_method="nearest")
cc

<ComparerCollection>
Comparers:
0: HKNA - Significant wave height [m]
1: EPL - Significant wave height [m]
2: c2 - Significant wave height [m]

cc["EPL"]   # select a single comparer from the collection like this

<Comparer>
Quantity: Significant wave height [m]
Observation: EPL, n_points=66
Model(s):
0: SW_1
1: SW_2
2: ERA5

Perform analysis

You can perform simple filtering on specific observation or specific model. You can refer to observations and models using their name or index.

The main analysis methods are:

• skill()

• mean_skill()

• scatter()

• taylor()

cc.skill()

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	HKNA	386	-0.194260	0.351964	0.293499	0.251839	0.971194	0.094489	0.905300
	EPL	66	-0.066028	0.224919	0.215009	0.189791	0.969512	0.082773	0.932082
	c2	102	-0.025059	0.354270	0.353383	0.297344	0.970862	0.131869	0.889056
SW_2	HKNA	386	-0.100426	0.293033	0.275287	0.214422	0.971194	0.088626	0.934358
	EPL	66	0.001181	0.233964	0.233961	0.199915	0.969512	0.090069	0.926509
	c2	102	0.050773	0.423351	0.420296	0.353069	0.970862	0.156839	0.841570
ERA5	HKNA	386	-0.437425	0.545329	0.325643	0.441374	0.974863	0.104837	0.772663
	EPL	66	-0.207731	0.289960	0.202299	0.223748	0.972255	0.077880	0.887121
	c2	102	-0.390274	0.486571	0.290582	0.407335	0.972701	0.108435	0.790720

cc.sel(observation="c2").skill()

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	c2	102	-0.025059	0.354270	0.353383	0.297344	0.970862	0.131869	0.889056
SW_2	c2	102	0.050773	0.423351	0.420296	0.353069	0.970862	0.156839	0.841570
ERA5	c2	102	-0.390274	0.486571	0.290582	0.407335	0.972701	0.108435	0.790720

cc.sel(model=0, observation=[0,"c2"]).mean_skill()

	n	bias	rmse	urmse	mae	cc	si	r2
model
ERA5	488	-0.413850	0.515950	0.308112	0.424354	0.973782	0.106636	0.781691
SW_1	488	-0.109659	0.353117	0.323441	0.274591	0.971028	0.113179	0.897178
SW_2	488	-0.024826	0.358192	0.347791	0.283745	0.971028	0.122732	0.887964

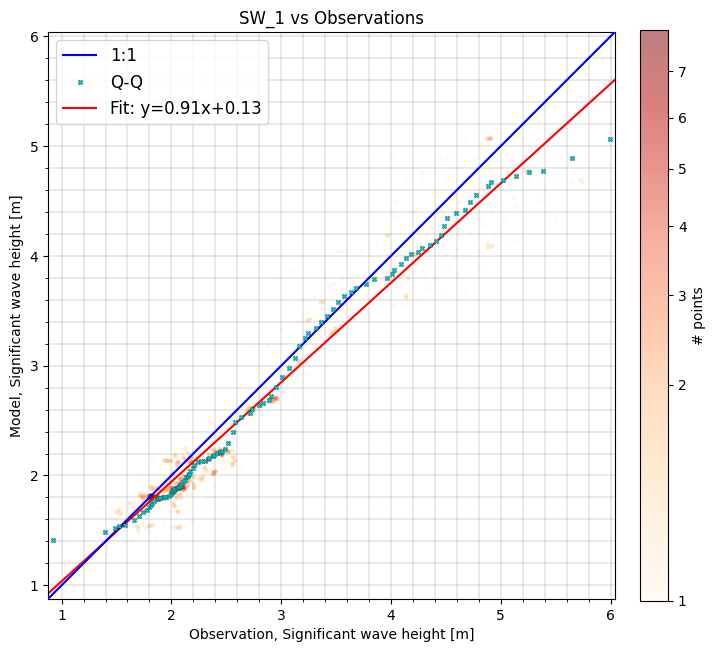
cc.sel(model='SW_1').plot.scatter(cmap='OrRd');

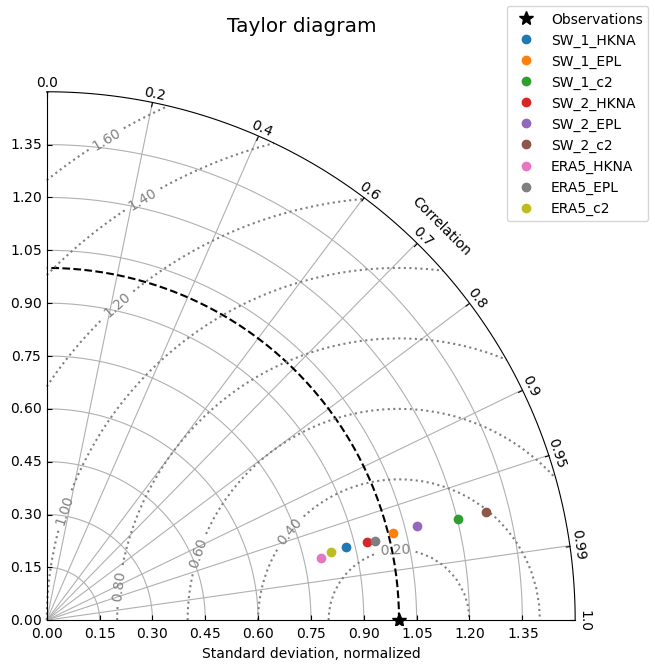
cc.plot.taylor(normalize_std=True, aggregate_observations=False)

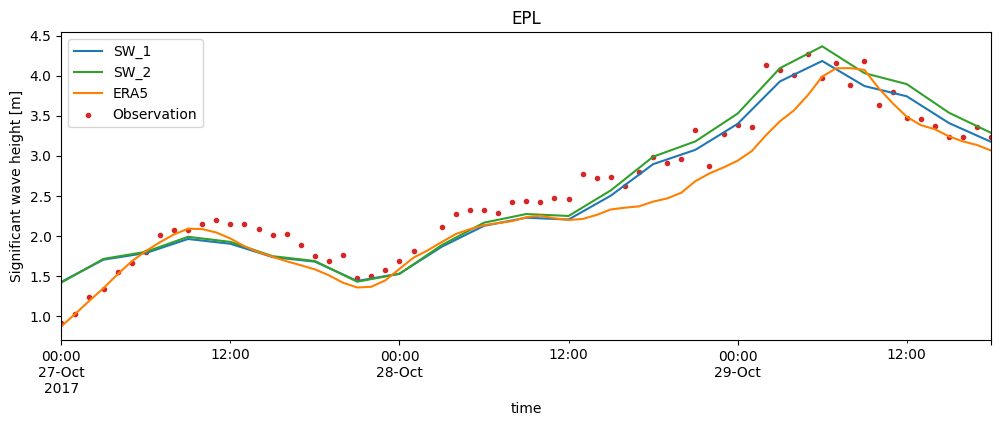
Time series plot (specifically for point comparisons)

If you select an comparison from the collection which is a PointComparer, you can do a time series plot

cc['EPL'].plot.timeseries(figsize=(12,4));

Filtering on time

Use the start and end arguments to do your analysis on part of the time series

cc.sel(model="SW_1", end='2017-10-28').skill()

	n	bias	rmse	urmse	mae	cc	si	r2
observation
HKNA	281	-0.097075	0.203241	0.178559	0.164563	0.968106	0.070167	0.916126
EPL	47	-0.100029	0.240775	0.219013	0.205827	0.919089	0.101695	0.811727
c2	66	-0.210375	0.323525	0.245786	0.268925	0.385374	0.121671	-1.855535

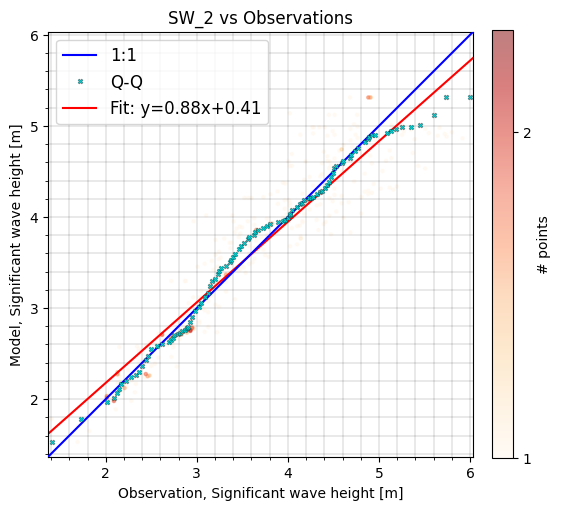
cc.sel(model='SW_2', start='2017-10-28').plot.scatter(cmap='OrRd', figsize=(6,7));

Filtering on area

You can do you analysis in a specific area by providing a bounding box or a closed polygon

bbox = np.array([0.5,52.5,5,54])
polygon = np.array([[6,51],[0,55],[0,51],[6,51]])

cc.sel(model="SW_1", area=bbox).skill()

	n	bias	rmse	urmse	mae	cc	si	r2
observation
HKNA	386	-0.19426	0.351964	0.293499	0.251839	0.971194	0.094489	0.905300
c2	42	-0.05587	0.388404	0.384365	0.336023	0.952688	0.145724	0.749645

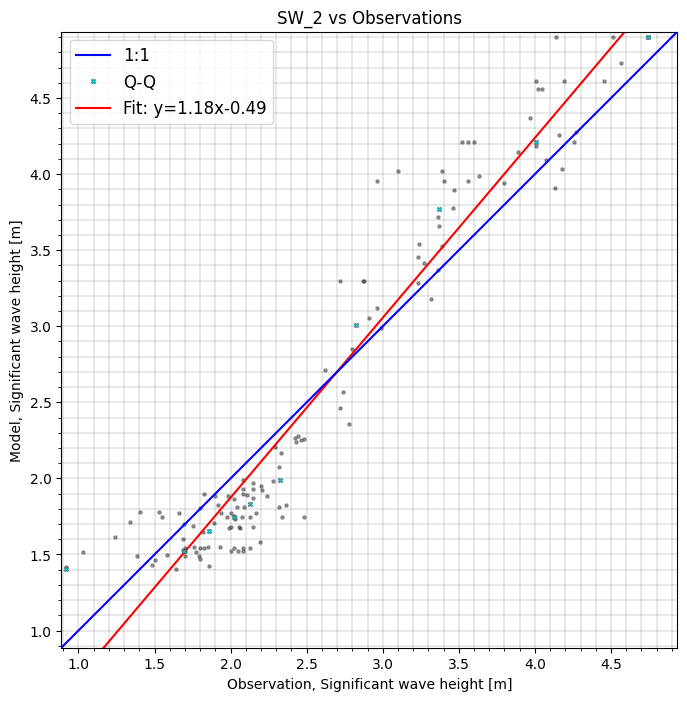
cc.sel(model="SW_2", area=polygon).plot.scatter();

Skill object

The skill() and mean_skill() methods return a skill object that can visualize results in various ways. The primary methods of the skill object are:

• style()

• plot_bar()

• plot_barh()

• plot_line()

• plot_grid()

• sel()

s = cc.skill()

s.style()

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	HKNA	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
	EPL	66	-0.066	0.225	0.215	0.190	0.970	0.083	0.932
	c2	102	-0.025	0.354	0.353	0.297	0.971	0.132	0.889
SW_2	HKNA	386	-0.100	0.293	0.275	0.214	0.971	0.089	0.934
	EPL	66	0.001	0.234	0.234	0.200	0.970	0.090	0.927
	c2	102	0.051	0.423	0.420	0.353	0.971	0.157	0.842
ERA5	HKNA	386	-0.437	0.545	0.326	0.441	0.975	0.105	0.773
	EPL	66	-0.208	0.290	0.202	0.224	0.972	0.078	0.887
	c2	102	-0.390	0.487	0.291	0.407	0.973	0.108	0.791

s.style(columns='rmse')

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	HKNA	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
	EPL	66	-0.066	0.225	0.215	0.190	0.970	0.083	0.932
	c2	102	-0.025	0.354	0.353	0.297	0.971	0.132	0.889
SW_2	HKNA	386	-0.100	0.293	0.275	0.214	0.971	0.089	0.934
	EPL	66	0.001	0.234	0.234	0.200	0.970	0.090	0.927
	c2	102	0.051	0.423	0.420	0.353	0.971	0.157	0.842
ERA5	HKNA	386	-0.437	0.545	0.326	0.441	0.975	0.105	0.773
	EPL	66	-0.208	0.290	0.202	0.224	0.972	0.078	0.887
	c2	102	-0.390	0.487	0.291	0.407	0.973	0.108	0.791

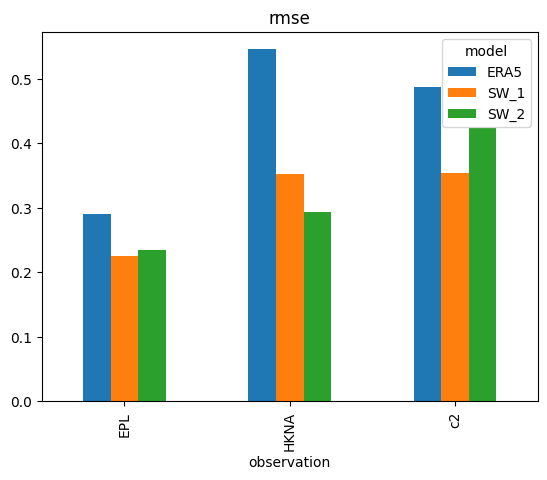
s['rmse'].plot.bar();
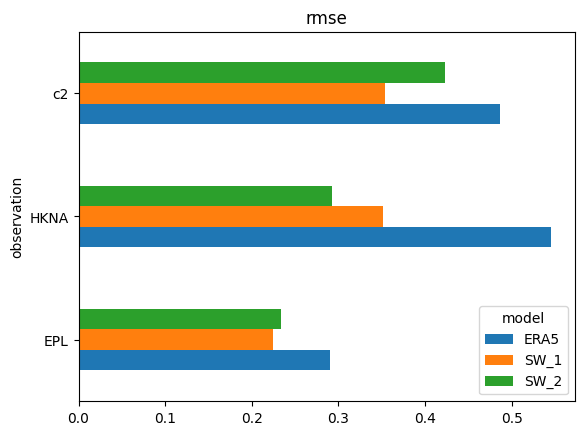
s['rmse'].plot.barh();  # horizontal version

s = cc.skill(by=['model','freq:12H'], metrics=['bias','rmse','si'])

s.style()

		n	bias	rmse	si
model	time
SW_1	2017-10-27 00:00:00	84	-0.096	0.257	0.117
	2017-10-27 12:00:00	150	-0.175	0.255	0.092
	2017-10-28 00:00:00	76	-0.111	0.179	0.057
	2017-10-28 12:00:00	84	-0.037	0.204	0.058
	2017-10-29 00:00:00	82	-0.421	0.596	0.089
	2017-10-29 12:00:00	78	-0.020	0.417	0.107
SW_2	2017-10-27 00:00:00	84	-0.070	0.236	0.110
	2017-10-27 12:00:00	150	-0.157	0.248	0.096
	2017-10-28 00:00:00	76	-0.055	0.150	0.056
	2017-10-28 12:00:00	84	0.091	0.234	0.063
	2017-10-29 00:00:00	82	-0.226	0.477	0.088
	2017-10-29 12:00:00	78	0.141	0.455	0.111
ERA5	2017-10-27 00:00:00	84	-0.161	0.205	0.062
	2017-10-27 12:00:00	150	-0.303	0.340	0.077
	2017-10-28 00:00:00	76	-0.200	0.264	0.069
	2017-10-28 12:00:00	84	-0.637	0.679	0.068
	2017-10-29 00:00:00	82	-0.699	0.800	0.082
	2017-10-29 12:00:00	78	-0.479	0.590	0.089

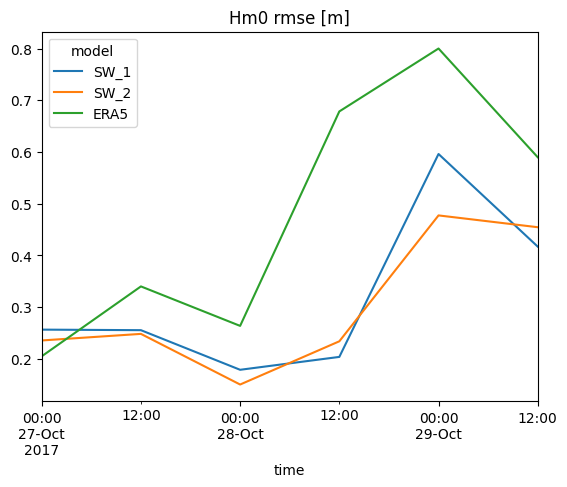
s['rmse'].plot.line(title='Hm0 rmse [m]');

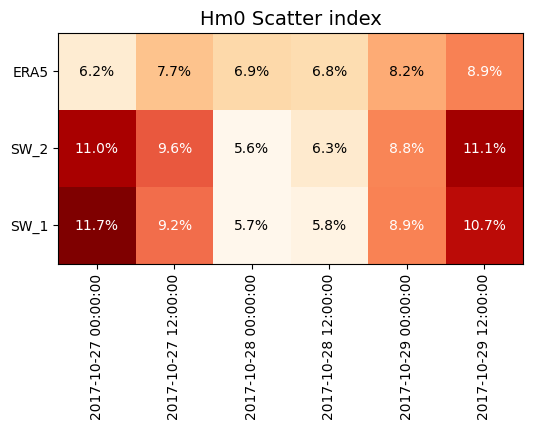
s.plot.grid('si', fmt='0.1%', title='Hm0 Scatter index');

/opt/hostedtoolcache/Python/3.9.18/x64/lib/python3.9/site-packages/modelskill/skill.py:279: FutureWarning: Selecting metric in plot functions like modelskill.skill().plot.grid(si) is deprecated and will be removed in a future version. Use modelskill.skill()['si'].plot.grid() instead.
  warnings.warn(

The sel() method can subset the skill object

A new skill object will be returned

s = cc.skill()
s.style()

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	HKNA	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
	EPL	66	-0.066	0.225	0.215	0.190	0.970	0.083	0.932
	c2	102	-0.025	0.354	0.353	0.297	0.971	0.132	0.889
SW_2	HKNA	386	-0.100	0.293	0.275	0.214	0.971	0.089	0.934
	EPL	66	0.001	0.234	0.234	0.200	0.970	0.090	0.927
	c2	102	0.051	0.423	0.420	0.353	0.971	0.157	0.842
ERA5	HKNA	386	-0.437	0.545	0.326	0.441	0.975	0.105	0.773
	EPL	66	-0.208	0.290	0.202	0.224	0.972	0.078	0.887
	c2	102	-0.390	0.487	0.291	0.407	0.973	0.108	0.791

s.sel(model='SW_1').style()

	model	n	bias	rmse	urmse	mae	cc	si	r2
observation
HKNA	SW_1	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
EPL	SW_1	66	-0.066	0.225	0.215	0.190	0.970	0.083	0.932
c2	SW_1	102	-0.025	0.354	0.353	0.297	0.971	0.132	0.889

s.sel(observation='HKNA').style()

	observation	n	bias	rmse	urmse	mae	cc	si	r2
model
SW_1	HKNA	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
SW_2	HKNA	386	-0.100	0.293	0.275	0.214	0.971	0.089	0.934
ERA5	HKNA	386	-0.437	0.545	0.326	0.441	0.975	0.105	0.773

s.query('rmse>0.25').style()

		n	bias	rmse	urmse	mae	cc	si	r2
model	observation
SW_1	HKNA	386	-0.194	0.352	0.293	0.252	0.971	0.094	0.905
	c2	102	-0.025	0.354	0.353	0.297	0.971	0.132	0.889
SW_2	HKNA	386	-0.100	0.293	0.275	0.214	0.971	0.089	0.934
	c2	102	0.051	0.423	0.420	0.353	0.971	0.157	0.842
ERA5	HKNA	386	-0.437	0.545	0.326	0.441	0.975	0.105	0.773
	EPL	66	-0.208	0.290	0.202	0.224	0.972	0.078	0.887
	c2	102	-0.390	0.487	0.291	0.407	0.973	0.108	0.791