Model skill assessment#
Simple comparison#
Sometimes all your need is a simple comparison of two time series. The modelskill.compare() method does just that.
import mikeio
import modelskill as ms
The model#
Can be either a dfs0 or a DataFrame.
fn_mod = 'data/SW/ts_storm_4.dfs0'
df_mod = mikeio.read(fn_mod, items=0).to_dataframe()
The observation#
Can be either a dfs0, a DataFrame or a PointObservation object.
fn_obs = 'data/SW/eur_Hm0.dfs0'
Match observation to model#
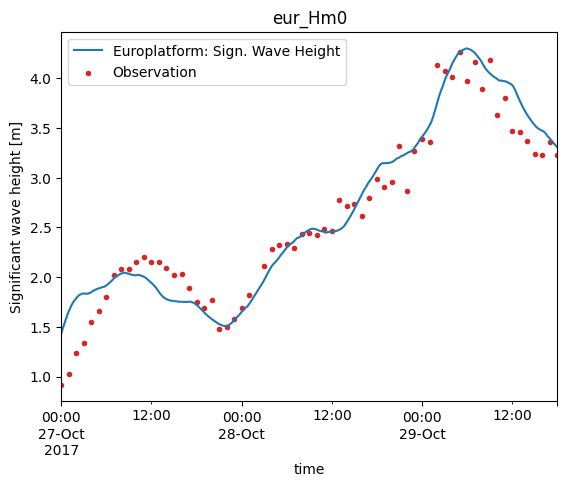
The match() method will return an object that can be used for scatter plots, skill assessment, time series plots etc.
cmp = ms.match(fn_obs, df_mod)
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/obs.py:79: UserWarning: Could not guess geometry type from data or args, assuming POINT geometry. Use PointObservation or TrackObservation to be explicit.
warnings.warn(
cmp.plot.timeseries();
Systematic vs random errors#
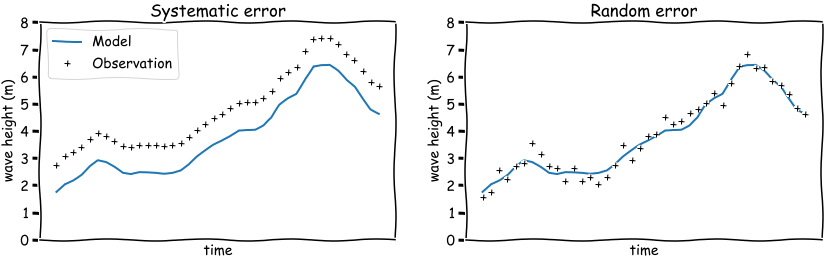
A model is an simplified version of a natural system, such as the ocean, and as such does not reflect every detail of the natural system.
In order to validate if a model does capture the essential dynamics of the natural system, it can be helpful to classify the mismatch of the model and observations in two broad categories:
systematic errors
random errors
A quantitativate assesment of a model involves calculating one or more model score, skill metrics, which in varying degrees capture systematic errors, random errors or a combination.
Metrics#
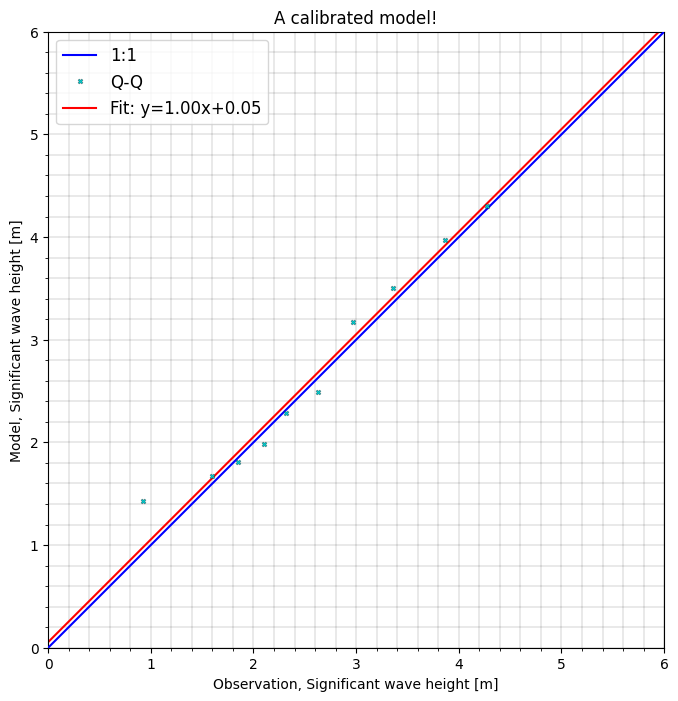
Bias is an indication of systematic error. In the left figure above, the model has negative bias (modelled wave heights are lower thatn observed). Thus it is an indication that the model can be improved.
Root Mean Square Error (rmse) is a combination of systematic and random error. It is a common metric to indicate the quality of a calibrated model, but less useful to understand the potential for further calibration since it captures both systematic and random errors.
Unbiased Root Mean Square Error (urmse) is the unbiased version of Root Mean Square Error. Since the bias is removed, it only captures the random error.
For a complete list of possible metrics, see the Metrics section in the ModelSkill docs.
To get a quantitative model skill, we use the .skill() method, which returns a table (similar to a DataFrame).
cmp.skill()
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/metrics.py:344: RuntimeWarning: divide by zero encountered in scalar divide
return 1 - SSr / SSt
| n | bias | rmse | urmse | mae | cc | si | r2 | |
|---|---|---|---|---|---|---|---|---|
| observation | ||||||||
| eur_Hm0 | 1 | 0.510124 | 0.510124 | 0.0 | 0.510124 | NaN | 0.0 | -inf |
The default is a number of common metrics, but you are free to pick your favorite metrics.
cmp.skill(metrics=["mae","rho","lin_slope"])
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/metrics.py:736: SmallSampleWarning: One or more sample arguments is too small; all returned values will be NaN. See documentation for sample size requirements.
reg = _linregress(obs, model)
| n | mae | rho | lin_slope | |
|---|---|---|---|---|
| observation | ||||
| eur_Hm0 | 1 | 0.510124 | NaN | NaN |
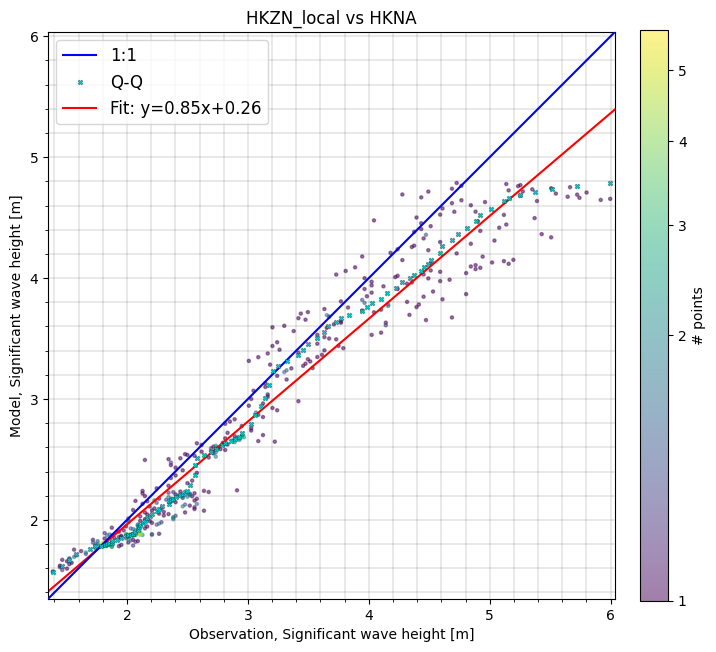
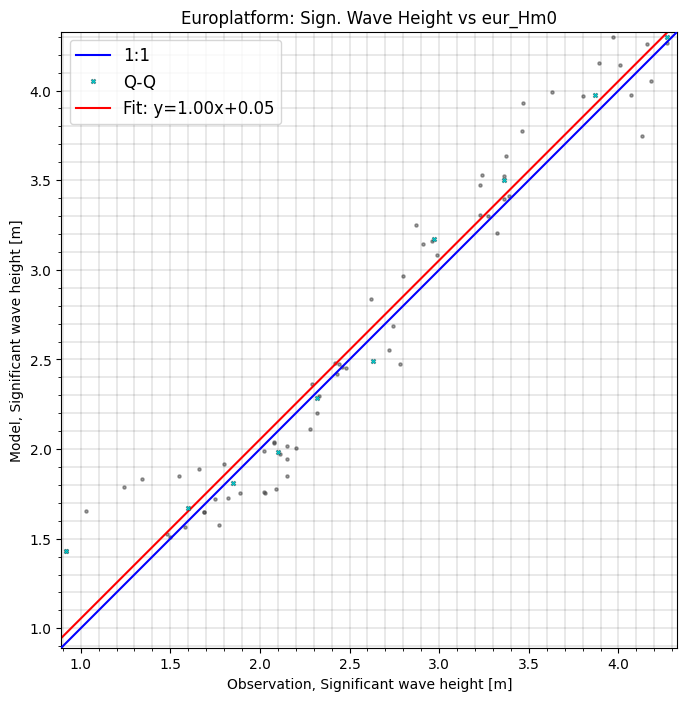
A very common way to visualize model skill is to use a scatter plot.
The scatter plot includes some additional features such as a 2d histogram, a Q-Q line and a regression line, but the appearance is highly configurable.
cmp.plot.scatter();
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[8], line 1
----> 1 cmp.plot.scatter();
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:565, in ComparerPlotter.scatter(self, model, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, ax, **kwargs)
563 axes = []
564 for mod_name in mod_names:
--> 565 ax_mod = self._scatter_one_model(
566 mod_name=mod_name,
567 bins=bins,
568 quantiles=quantiles,
569 fit_to_quantiles=fit_to_quantiles,
570 show_points=show_points,
571 show_hist=show_hist,
572 show_density=show_density,
573 norm=norm,
574 backend=backend,
575 figsize=figsize,
576 xlim=xlim,
577 ylim=ylim,
578 reg_method=reg_method,
579 title=title,
580 xlabel=xlabel,
581 ylabel=ylabel,
582 skill_table=skill_table,
583 ax=ax,
584 **kwargs,
585 )
586 axes.append(ax_mod)
587 return axes[0] if len(axes) == 1 else axes
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:649, in ComparerPlotter._scatter_one_model(self, mod_name, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, **kwargs)
645 reg_method = False
647 skill_scores = skill.iloc[0].to_dict() if skill is not None else None
--> 649 ax = scatter(
650 x=x,
651 y=y,
652 bins=bins,
653 quantiles=quantiles,
654 fit_to_quantiles=fit_to_quantiles,
655 show_points=show_points,
656 show_hist=show_hist,
657 show_density=show_density,
658 norm=norm,
659 backend=backend,
660 figsize=figsize,
661 xlim=xlim,
662 ylim=ylim,
663 reg_method=reg_method,
664 title=title,
665 xlabel=xlabel,
666 ylabel=ylabel,
667 skill_scores=skill_scores,
668 skill_score_unit=skill_score_unit,
669 **kwargs,
670 )
672 if backend == "matplotlib" and self.is_directional:
673 _xtick_directional(ax, xlim)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:228, in scatter(x, y, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, skill_scores, skill_score_unit, ax, **kwargs)
225 skill = cmp.skill(metrics=metrics)
226 skill_scores = skill.to_dict("records")[0]
--> 228 return PLOTTING_BACKENDS[backend](
229 x=x,
230 y=y,
231 x_sample=x_sample,
232 y_sample=y_sample,
233 z=z,
234 xq=xq,
235 yq=yq,
236 x_trend=x_trend,
237 show_density=show_density,
238 norm=norm,
239 show_points=show_points,
240 show_hist=show_hist,
241 nbins_hist=nbins_hist,
242 reg_method=reg_method,
243 xlabel=xlabel,
244 ylabel=ylabel,
245 figsize=figsize,
246 xlim=xlim,
247 ylim=ylim,
248 title=title,
249 skill_scores=skill_scores,
250 skill_score_unit=skill_score_unit,
251 fit_to_quantiles=fit_to_quantiles,
252 ax=ax,
253 **kwargs,
254 )
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:289, in _scatter_matplotlib(x, y, x_sample, y_sample, z, xq, yq, x_trend, show_density, show_points, show_hist, norm, nbins_hist, reg_method, xlabel, ylabel, figsize, xlim, ylim, title, skill_scores, skill_score_unit, fit_to_quantiles, ax, cmap, **kwargs)
286 fig, ax = _get_fig_ax(ax, figsize)
288 if len(x) < 2:
--> 289 raise ValueError("Not enough data to plot. At least 2 points are required.")
291 ax.plot(
292 [xlim[0], xlim[1]],
293 [xlim[0], xlim[1]],
(...) 296 zorder=3,
297 )
299 if show_points is None or show_points:
ValueError: Not enough data to plot. At least 2 points are required.
cmp.plot.scatter(binsize=0.5,
show_points=False,
xlim=[0,6], ylim=[0,6],
title="A calibrated model!");
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[9], line 1
----> 1 cmp.plot.scatter(binsize=0.5,
2 show_points=False,
3 xlim=[0,6], ylim=[0,6],
4 title="A calibrated model!");
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:565, in ComparerPlotter.scatter(self, model, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, ax, **kwargs)
563 axes = []
564 for mod_name in mod_names:
--> 565 ax_mod = self._scatter_one_model(
566 mod_name=mod_name,
567 bins=bins,
568 quantiles=quantiles,
569 fit_to_quantiles=fit_to_quantiles,
570 show_points=show_points,
571 show_hist=show_hist,
572 show_density=show_density,
573 norm=norm,
574 backend=backend,
575 figsize=figsize,
576 xlim=xlim,
577 ylim=ylim,
578 reg_method=reg_method,
579 title=title,
580 xlabel=xlabel,
581 ylabel=ylabel,
582 skill_table=skill_table,
583 ax=ax,
584 **kwargs,
585 )
586 axes.append(ax_mod)
587 return axes[0] if len(axes) == 1 else axes
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:649, in ComparerPlotter._scatter_one_model(self, mod_name, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, **kwargs)
645 reg_method = False
647 skill_scores = skill.iloc[0].to_dict() if skill is not None else None
--> 649 ax = scatter(
650 x=x,
651 y=y,
652 bins=bins,
653 quantiles=quantiles,
654 fit_to_quantiles=fit_to_quantiles,
655 show_points=show_points,
656 show_hist=show_hist,
657 show_density=show_density,
658 norm=norm,
659 backend=backend,
660 figsize=figsize,
661 xlim=xlim,
662 ylim=ylim,
663 reg_method=reg_method,
664 title=title,
665 xlabel=xlabel,
666 ylabel=ylabel,
667 skill_scores=skill_scores,
668 skill_score_unit=skill_score_unit,
669 **kwargs,
670 )
672 if backend == "matplotlib" and self.is_directional:
673 _xtick_directional(ax, xlim)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:228, in scatter(x, y, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, skill_scores, skill_score_unit, ax, **kwargs)
225 skill = cmp.skill(metrics=metrics)
226 skill_scores = skill.to_dict("records")[0]
--> 228 return PLOTTING_BACKENDS[backend](
229 x=x,
230 y=y,
231 x_sample=x_sample,
232 y_sample=y_sample,
233 z=z,
234 xq=xq,
235 yq=yq,
236 x_trend=x_trend,
237 show_density=show_density,
238 norm=norm,
239 show_points=show_points,
240 show_hist=show_hist,
241 nbins_hist=nbins_hist,
242 reg_method=reg_method,
243 xlabel=xlabel,
244 ylabel=ylabel,
245 figsize=figsize,
246 xlim=xlim,
247 ylim=ylim,
248 title=title,
249 skill_scores=skill_scores,
250 skill_score_unit=skill_score_unit,
251 fit_to_quantiles=fit_to_quantiles,
252 ax=ax,
253 **kwargs,
254 )
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:289, in _scatter_matplotlib(x, y, x_sample, y_sample, z, xq, yq, x_trend, show_density, show_points, show_hist, norm, nbins_hist, reg_method, xlabel, ylabel, figsize, xlim, ylim, title, skill_scores, skill_score_unit, fit_to_quantiles, ax, cmap, **kwargs)
286 fig, ax = _get_fig_ax(ax, figsize)
288 if len(x) < 2:
--> 289 raise ValueError("Not enough data to plot. At least 2 points are required.")
291 ax.plot(
292 [xlim[0], xlim[1]],
293 [xlim[0], xlim[1]],
(...) 296 zorder=3,
297 )
299 if show_points is None or show_points:
ValueError: Not enough data to plot. At least 2 points are required.
Taylor diagram#
A taylor diagram is a way to combine several statistics in a single plot, and is very useful to compare the skill of several models, or observations in a single plot.
cmp.plot.taylor();
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[10], line 1
----> 1 cmp.plot.taylor();
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:754, in ComparerPlotter.taylor(self, normalize_std, figsize, marker, marker_size, title)
748 pts = [
749 TaylorPoint(name=r.model, obs_std=r.obs_std, std=r.std, cc=r.cc, marker=marker, marker_size=marker_size)
750 for r in df.itertuples()
751 ]
753 # TODO consistent return type with other plotting methods
--> 754 return taylor_diagram(
755 obs_std=ref_std,
756 points=pts,
757 figsize=figsize,
758 obs_text=f"Obs: {cmp.name}",
759 normalize_std=normalize_std,
760 title=title,
761 )
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_taylor_diagram.py:68, in taylor_diagram(obs_std, points, figsize, obs_text, normalize_std, ax, title)
65 if len(obs_text) > 30:
66 obs_text = obs_text[:25] + "..."
---> 68 td = TaylorDiagram(
69 obs_std, fig=fig, rect=111, label=obs_text, normalize_std=normalize_std
70 )
71 contours = td.add_contours(levels=8, colors="0.5", linestyles="dotted")
72 plt.clabel(contours, inline=1, fontsize=10, fmt="%.2f")
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_taylor_diagram_external.py:87, in TaylorDiagram.__init__(self, refstd, fig, rect, label, srange, extend, normalize_std)
84 if fig is None:
85 fig = plt.figure()
---> 87 ax = FA.FloatingSubplot(fig, rect, grid_helper=ghelper)
88 fig.add_subplot(ax)
90 # Adjust axes
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mpl_toolkits/axisartist/floating_axes.py:240, in FloatingAxesBase.__init__(self, grid_helper, *args, **kwargs)
238 def __init__(self, *args, grid_helper, **kwargs):
239 _api.check_isinstance(GridHelperCurveLinear, grid_helper=grid_helper)
--> 240 super().__init__(*args, grid_helper=grid_helper, **kwargs)
241 self.set_aspect(1.)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mpl_toolkits/axes_grid1/parasite_axes.py:83, in HostAxesBase.__init__(self, *args, **kwargs)
81 def __init__(self, *args, **kwargs):
82 self.parasites = []
---> 83 super().__init__(*args, **kwargs)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mpl_toolkits/axisartist/axislines.py:376, in Axes.__init__(self, grid_helper, *args, **kwargs)
374 self._axisline_on = True
375 self._grid_helper = grid_helper if grid_helper else GridHelperRectlinear(self)
--> 376 super().__init__(*args, **kwargs)
377 self.toggle_axisline(True)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/axes/_base.py:732, in _AxesBase.__init__(self, fig, facecolor, frameon, sharex, sharey, label, xscale, yscale, box_aspect, forward_navigation_events, *args, **kwargs)
729 self.set_axisbelow(mpl.rcParams['axes.axisbelow'])
731 self._rasterization_zorder = None
--> 732 self.clear()
734 # funcs used to format x and y - fall back on major formatters
735 self.fmt_xdata = None
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mpl_toolkits/axisartist/floating_axes.py:262, in FloatingAxesBase.clear(self)
260 self.patch.set_clip_path(orig_patch)
261 self.gridlines.set_clip_path(orig_patch)
--> 262 self.adjust_axes_lim()
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mpl_toolkits/axisartist/floating_axes.py:265, in FloatingAxesBase.adjust_axes_lim(self)
264 def adjust_axes_lim(self):
--> 265 bbox = self.patch.get_path().get_extents(
266 # First transform to pixel coords, then to parent data coords.
267 self.patch.get_transform() - self.transData)
268 bbox = bbox.expanded(1.02, 1.02)
269 self.set_xlim(bbox.xmin, bbox.xmax)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/path.py:645, in Path.get_extents(self, transform, **kwargs)
643 from .transforms import Bbox
644 if transform is not None:
--> 645 self = transform.transform_path(self)
646 if self.codes is None:
647 xys = self.vertices
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/transforms.py:1601, in Transform.transform_path(self, path)
1594 def transform_path(self, path):
1595 """
1596 Apply the transform to `.Path` *path*, returning a new `.Path`.
1597
1598 In some cases, this transform may insert curves into the path
1599 that began as line segments.
1600 """
-> 1601 return self.transform_path_affine(self.transform_path_non_affine(path))
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/projections/polar.py:147, in PolarTransform.transform_path_non_affine(self, path)
145 codes.extend([c] * len(trs))
146 last_t, last_r = trs[-1]
--> 147 return Path(xys, codes)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/path.py:130, in Path.__init__(self, vertices, codes, _interpolation_steps, closed, readonly)
101 """
102 Create a new path with the given vertices and codes.
103
(...) 127 and codes as read-only arrays.
128 """
129 vertices = _to_unmasked_float_array(vertices)
--> 130 _api.check_shape((None, 2), vertices=vertices)
132 if codes is not None and len(vertices):
133 codes = np.asarray(codes, self.code_type)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/matplotlib/_api/__init__.py:176, in check_shape(shape, **kwargs)
173 if len(shape) == 1:
174 text_shape += ","
--> 176 raise ValueError(
177 f"{k!r} must be {len(shape)}D with shape ({text_shape}), "
178 f"but your input has shape {v.shape}"
179 )
ValueError: 'vertices' must be 2D with shape (N, 2), but your input has shape (0,)
<Figure size 700x700 with 0 Axes>
Elaborate comparison#
fn = 'data/SW/HKZN_local_2017_DutchCoast.dfsu'
mr = ms.model_result(fn, name='HKZN_local', item=0)
mr
<DfsuModelResult>: HKZN_local
Time: 2017-10-27 00:00:00 - 2017-10-29 18:00:00
Quantity: Significant wave height [m]
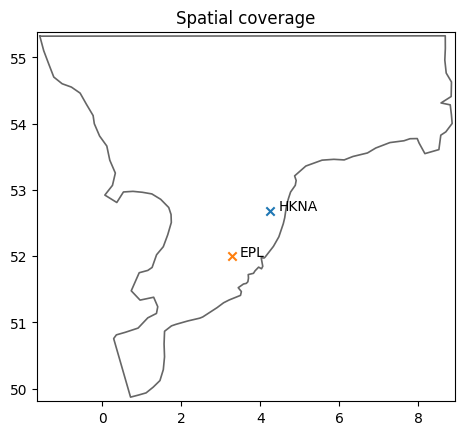
o1 = ms.PointObservation('data/SW/HKNA_Hm0.dfs0', item=0, x=4.2420, y=52.6887, name="HKNA")
o2 = ms.PointObservation("data/SW/eur_Hm0.dfs0", item=0, x=3.2760, y=51.9990, name="EPL")
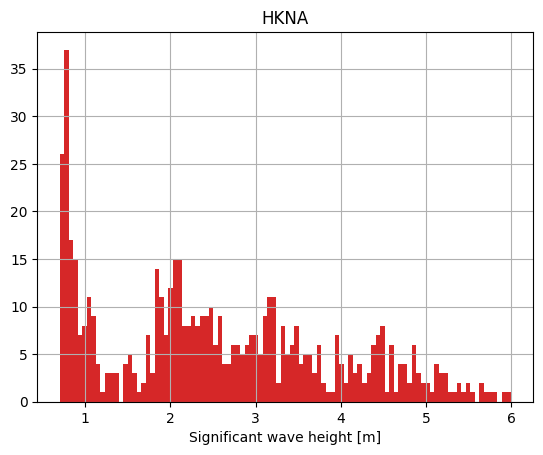
o1.plot.hist();
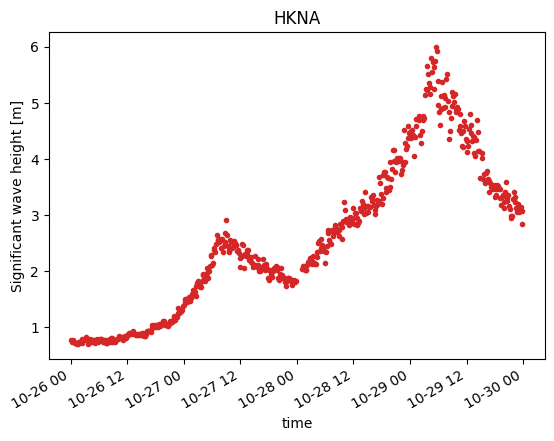
o1.plot();
Overview#
ms.plotting.spatial_overview(obs=[o1,o2], mod=mr);
cc = ms.match(obs=[o1,o2], mod=mr)
cc
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mikeio/dataset/_dataset.py:505: FutureWarning: 'inplace' parameter is deprecated and will be removed in future versions. Use ds = ds.rename(...) instead.
warnings.warn(
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/mikeio/dataset/_dataset.py:505: FutureWarning: 'inplace' parameter is deprecated and will be removed in future versions. Use ds = ds.rename(...) instead.
warnings.warn(
<ComparerCollection>
Comparers:
0: HKNA - Significant wave height [m]
1: EPL - Significant wave height [m]
cc.skill().style(precision=2)
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/metrics.py:344: RuntimeWarning: divide by zero encountered in scalar divide
return 1 - SSr / SSt
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/skill.py:804: FutureWarning: precision is deprecated, it has been renamed to decimals
warnings.warn(
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/pandas/io/formats/style.py:4202: RuntimeWarning: All-NaN slice encountered
smin = np.nanmin(gmap) if vmin is None else vmin
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/pandas/io/formats/style.py:4203: RuntimeWarning: All-NaN slice encountered
smax = np.nanmax(gmap) if vmax is None else vmax
/opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/pandas/io/formats/style.py:4204: RuntimeWarning: invalid value encountered in scalar subtract
rng = smax - smin
| n | bias | rmse | urmse | mae | cc | si | r2 | |
|---|---|---|---|---|---|---|---|---|
| observation | ||||||||
| HKNA | 1 | 0.19 | 0.19 | 0.00 | 0.19 | nan | 0.00 | -inf |
| EPL | 1 | 0.52 | 0.52 | 0.00 | 0.52 | nan | 0.00 | -inf |
cc["EPL"].skill(metrics="mean_absolute_error")
| n | mean_absolute_error | |
|---|---|---|
| observation | ||
| EPL | 1 | 0.518057 |
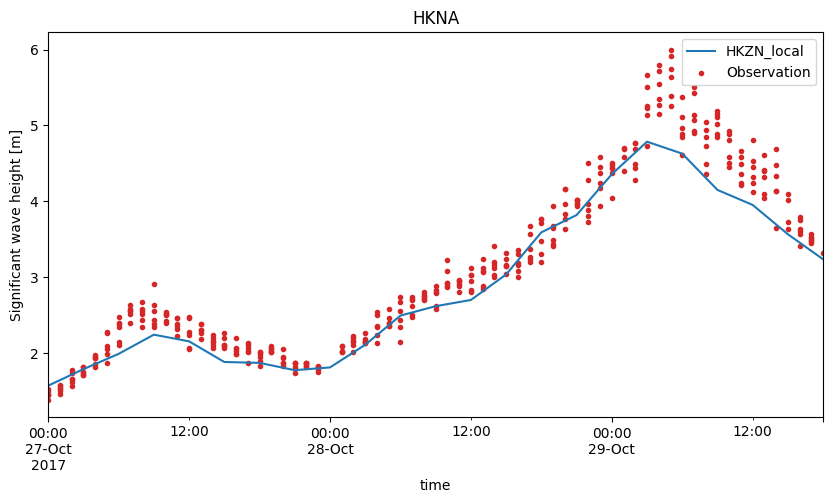
cc["HKNA"].plot.timeseries(figsize=(10,5));
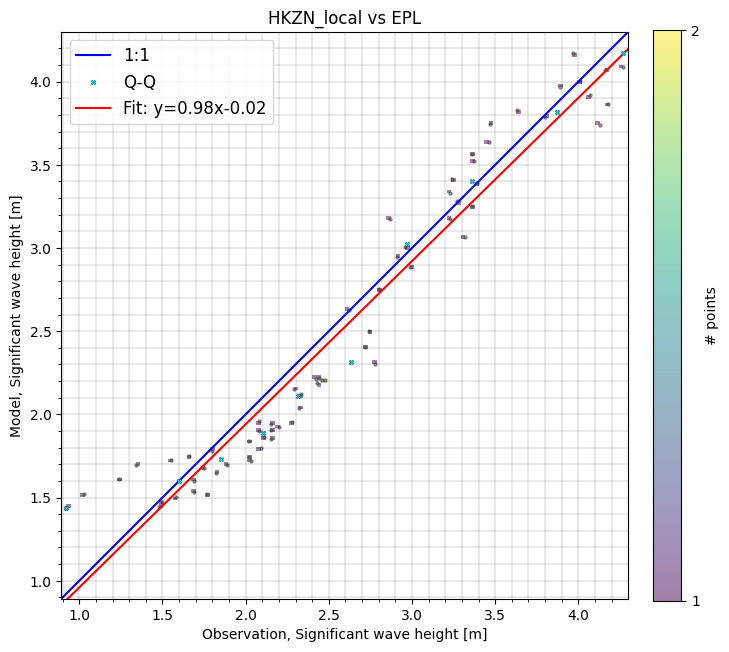
cc["EPL"].plot.scatter(figsize=(8,8), show_hist=True);
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[20], line 1
----> 1 cc["EPL"].plot.scatter(figsize=(8,8), show_hist=True);
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:565, in ComparerPlotter.scatter(self, model, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, ax, **kwargs)
563 axes = []
564 for mod_name in mod_names:
--> 565 ax_mod = self._scatter_one_model(
566 mod_name=mod_name,
567 bins=bins,
568 quantiles=quantiles,
569 fit_to_quantiles=fit_to_quantiles,
570 show_points=show_points,
571 show_hist=show_hist,
572 show_density=show_density,
573 norm=norm,
574 backend=backend,
575 figsize=figsize,
576 xlim=xlim,
577 ylim=ylim,
578 reg_method=reg_method,
579 title=title,
580 xlabel=xlabel,
581 ylabel=ylabel,
582 skill_table=skill_table,
583 ax=ax,
584 **kwargs,
585 )
586 axes.append(ax_mod)
587 return axes[0] if len(axes) == 1 else axes
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:649, in ComparerPlotter._scatter_one_model(self, mod_name, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, **kwargs)
645 reg_method = False
647 skill_scores = skill.iloc[0].to_dict() if skill is not None else None
--> 649 ax = scatter(
650 x=x,
651 y=y,
652 bins=bins,
653 quantiles=quantiles,
654 fit_to_quantiles=fit_to_quantiles,
655 show_points=show_points,
656 show_hist=show_hist,
657 show_density=show_density,
658 norm=norm,
659 backend=backend,
660 figsize=figsize,
661 xlim=xlim,
662 ylim=ylim,
663 reg_method=reg_method,
664 title=title,
665 xlabel=xlabel,
666 ylabel=ylabel,
667 skill_scores=skill_scores,
668 skill_score_unit=skill_score_unit,
669 **kwargs,
670 )
672 if backend == "matplotlib" and self.is_directional:
673 _xtick_directional(ax, xlim)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:228, in scatter(x, y, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, skill_scores, skill_score_unit, ax, **kwargs)
225 skill = cmp.skill(metrics=metrics)
226 skill_scores = skill.to_dict("records")[0]
--> 228 return PLOTTING_BACKENDS[backend](
229 x=x,
230 y=y,
231 x_sample=x_sample,
232 y_sample=y_sample,
233 z=z,
234 xq=xq,
235 yq=yq,
236 x_trend=x_trend,
237 show_density=show_density,
238 norm=norm,
239 show_points=show_points,
240 show_hist=show_hist,
241 nbins_hist=nbins_hist,
242 reg_method=reg_method,
243 xlabel=xlabel,
244 ylabel=ylabel,
245 figsize=figsize,
246 xlim=xlim,
247 ylim=ylim,
248 title=title,
249 skill_scores=skill_scores,
250 skill_score_unit=skill_score_unit,
251 fit_to_quantiles=fit_to_quantiles,
252 ax=ax,
253 **kwargs,
254 )
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:289, in _scatter_matplotlib(x, y, x_sample, y_sample, z, xq, yq, x_trend, show_density, show_points, show_hist, norm, nbins_hist, reg_method, xlabel, ylabel, figsize, xlim, ylim, title, skill_scores, skill_score_unit, fit_to_quantiles, ax, cmap, **kwargs)
286 fig, ax = _get_fig_ax(ax, figsize)
288 if len(x) < 2:
--> 289 raise ValueError("Not enough data to plot. At least 2 points are required.")
291 ax.plot(
292 [xlim[0], xlim[1]],
293 [xlim[0], xlim[1]],
(...) 296 zorder=3,
297 )
299 if show_points is None or show_points:
ValueError: Not enough data to plot. At least 2 points are required.
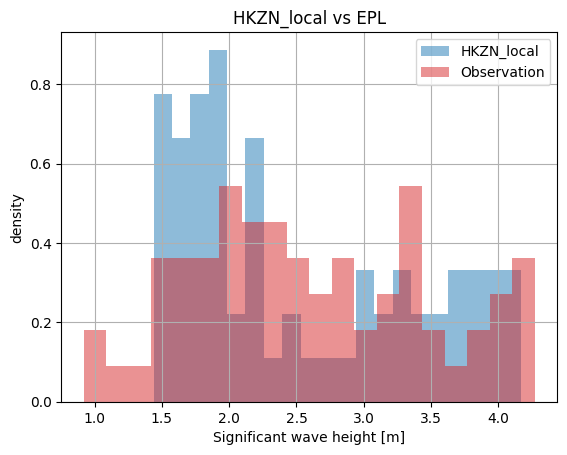
cc["EPL"].plot.hist(bins=20);
cc["HKNA"].plot.scatter();
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[22], line 1
----> 1 cc["HKNA"].plot.scatter();
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:565, in ComparerPlotter.scatter(self, model, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, ax, **kwargs)
563 axes = []
564 for mod_name in mod_names:
--> 565 ax_mod = self._scatter_one_model(
566 mod_name=mod_name,
567 bins=bins,
568 quantiles=quantiles,
569 fit_to_quantiles=fit_to_quantiles,
570 show_points=show_points,
571 show_hist=show_hist,
572 show_density=show_density,
573 norm=norm,
574 backend=backend,
575 figsize=figsize,
576 xlim=xlim,
577 ylim=ylim,
578 reg_method=reg_method,
579 title=title,
580 xlabel=xlabel,
581 ylabel=ylabel,
582 skill_table=skill_table,
583 ax=ax,
584 **kwargs,
585 )
586 axes.append(ax_mod)
587 return axes[0] if len(axes) == 1 else axes
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/comparison/_comparer_plotter.py:649, in ComparerPlotter._scatter_one_model(self, mod_name, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, **kwargs)
645 reg_method = False
647 skill_scores = skill.iloc[0].to_dict() if skill is not None else None
--> 649 ax = scatter(
650 x=x,
651 y=y,
652 bins=bins,
653 quantiles=quantiles,
654 fit_to_quantiles=fit_to_quantiles,
655 show_points=show_points,
656 show_hist=show_hist,
657 show_density=show_density,
658 norm=norm,
659 backend=backend,
660 figsize=figsize,
661 xlim=xlim,
662 ylim=ylim,
663 reg_method=reg_method,
664 title=title,
665 xlabel=xlabel,
666 ylabel=ylabel,
667 skill_scores=skill_scores,
668 skill_score_unit=skill_score_unit,
669 **kwargs,
670 )
672 if backend == "matplotlib" and self.is_directional:
673 _xtick_directional(ax, xlim)
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:228, in scatter(x, y, bins, quantiles, fit_to_quantiles, show_points, show_hist, show_density, norm, backend, figsize, xlim, ylim, reg_method, title, xlabel, ylabel, skill_table, skill_scores, skill_score_unit, ax, **kwargs)
225 skill = cmp.skill(metrics=metrics)
226 skill_scores = skill.to_dict("records")[0]
--> 228 return PLOTTING_BACKENDS[backend](
229 x=x,
230 y=y,
231 x_sample=x_sample,
232 y_sample=y_sample,
233 z=z,
234 xq=xq,
235 yq=yq,
236 x_trend=x_trend,
237 show_density=show_density,
238 norm=norm,
239 show_points=show_points,
240 show_hist=show_hist,
241 nbins_hist=nbins_hist,
242 reg_method=reg_method,
243 xlabel=xlabel,
244 ylabel=ylabel,
245 figsize=figsize,
246 xlim=xlim,
247 ylim=ylim,
248 title=title,
249 skill_scores=skill_scores,
250 skill_score_unit=skill_score_unit,
251 fit_to_quantiles=fit_to_quantiles,
252 ax=ax,
253 **kwargs,
254 )
File /opt/hostedtoolcache/Python/3.13.12/x64/lib/python3.13/site-packages/modelskill/plotting/_scatter.py:289, in _scatter_matplotlib(x, y, x_sample, y_sample, z, xq, yq, x_trend, show_density, show_points, show_hist, norm, nbins_hist, reg_method, xlabel, ylabel, figsize, xlim, ylim, title, skill_scores, skill_score_unit, fit_to_quantiles, ax, cmap, **kwargs)
286 fig, ax = _get_fig_ax(ax, figsize)
288 if len(x) < 2:
--> 289 raise ValueError("Not enough data to plot. At least 2 points are required.")
291 ax.plot(
292 [xlim[0], xlim[1]],
293 [xlim[0], xlim[1]],
(...) 296 zorder=3,
297 )
299 if show_points is None or show_points:
ValueError: Not enough data to plot. At least 2 points are required.