Mesh

See Mesh in MIKE IO Documentation

import numpy as np
import matplotlib.pyplot as plt
import mikeio

A simple mesh

Let’s consider a simple mesh consisting of 2 triangular elements.

Note

Example data can be found in the mini_book/data folder in this zip-file.

fn = "data/two_elements.mesh"

with open(fn, "r") as f:
    print(f.read())

100079 1000 4  UTM-31
1 0.0 0.0 -10.0 1 
2 3.0 0.0 -10.0 2 
3 3.0 3.0 -10.0 2 
4 0.0 3.0 -10.0 1 
2 3 21
1 1 2 4
2 2 3 4 

msh = mikeio.open(fn)
msh

<Mesh>
number of nodes: 4
number of elements: 2
projection: UTM-31

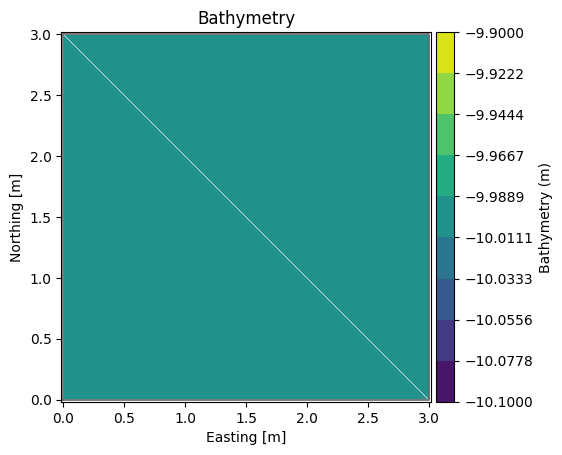
msh.plot(show_mesh=True);

msh.node_coordinates

array([[  0.,   0., -10.],
       [  3.,   0., -10.],
       [  3.,   3., -10.],
       [  0.,   3., -10.]])

msh.element_table

[array([0, 1, 3], dtype=int32), array([1, 2, 3], dtype=int32)]

msh.element_coordinates

array([[  1.,   1., -10.],
       [  2.,   2., -10.]])

msh.geometry.get_element_area()

array([4.5, 4.5])

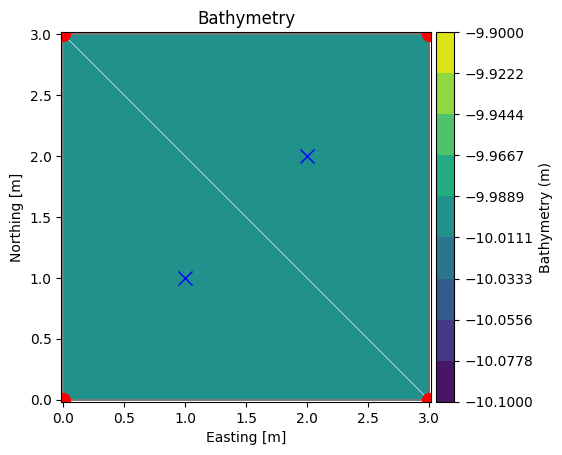
Let’s plot the node and element coordinates:

xn, yn = msh.node_coordinates[:,0], msh.node_coordinates[:,1]
xe, ye = msh.element_coordinates[:,0], msh.element_coordinates[:,1]

ax = msh.plot(show_mesh=True)
ax.plot(xn, yn, 'ro', markersize=10)
ax.plot(xe, ye, 'bx', markersize=10)

[<matplotlib.lines.Line2D at 0x7fe727994050>]

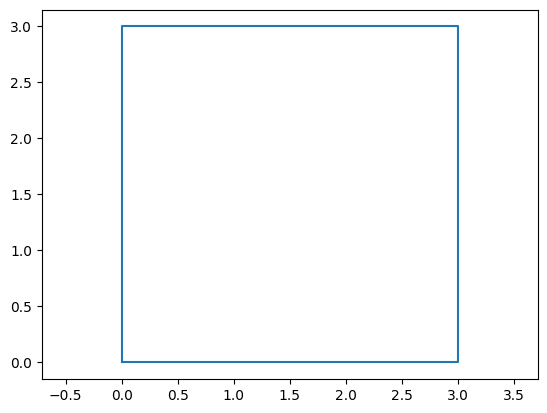
Boundary polygons

It can sometimes be convenient to have mesh boundary as a polygon (or multiple in case of more complex meshes).

bxy = msh.geometry.boundary_polygons.exteriors[0].xy
plt.plot(bxy[:,0], bxy[:,1])
plt.axis("equal");

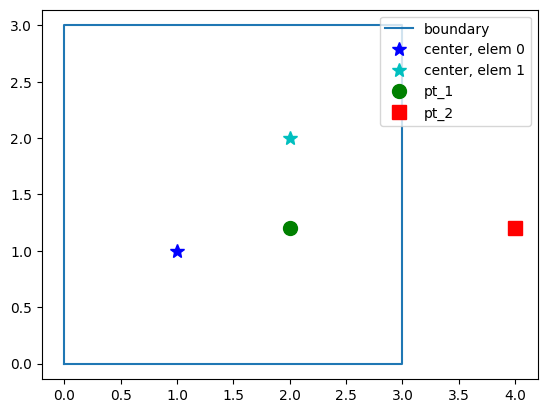
Inside domain?

MIKE IO has a method for determining if a point (or a list of points) is inside the domain:

• contains()

pt_1 = [2.0, 1.2]
msh.geometry.contains(pt_1)[0]

np.True_

# or multiple points at the same time
pt_2 = [4.0, 1.2]
pts = np.array([pt_1, pt_2])
msh.geometry.contains(pts)

array([ True, False])

plt.plot(bxy[:,0], bxy[:,1], label='boundary')
plt.plot(xe[0], ye[0], 'b*', markersize=10, label="center, elem 0")
plt.plot(xe[1], ye[1], 'c*', markersize=10, label="center, elem 1")
plt.plot(*pt_1, 'go', markersize=10, label="pt_1")
plt.plot(*pt_2, 'rs', markersize=10, label="pt_2")
plt.axis("equal")
plt.legend(loc="upper right");

Find element containing point

MIKE IO has a method for obtaining the index of the element containing a point:

• find_index()

g = msh.geometry
g.find_index(coords=pt_1)[0]

np.int64(1)

MIKE IO also has a method for obtaining a list of the n closest element centers:

• find_nearest_elements()

g.find_nearest_elements(pt_1)

1

g.find_nearest_elements(pt_1, return_distances=True)

(1, 0.8)

g.find_nearest_elements(pt_1, n_nearest=2)

array([1, 0])

# for multiple points
g.find_nearest_elements(pts, return_distances=True)

(array([1, 1]), array([0.8       , 2.15406592]))

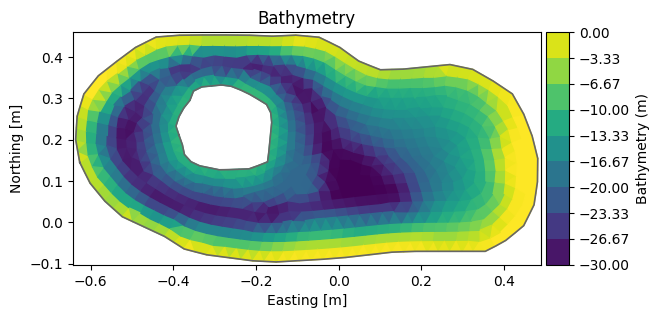
A larger mesh

A dfsu file also has a flexible mesh geometry attribute.

fn = "data/FakeLake.dfsu"
dfs = mikeio.open(fn)
g = dfs.geometry

g.plot();

g.max_nodes_per_element

4

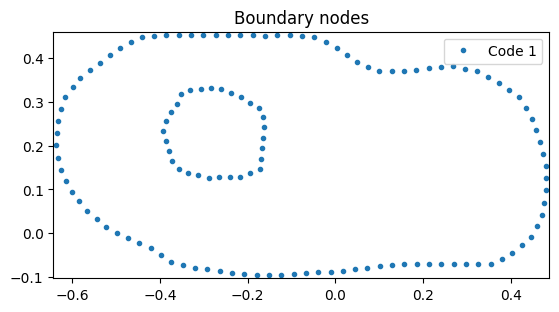
g.plot.boundary_nodes();

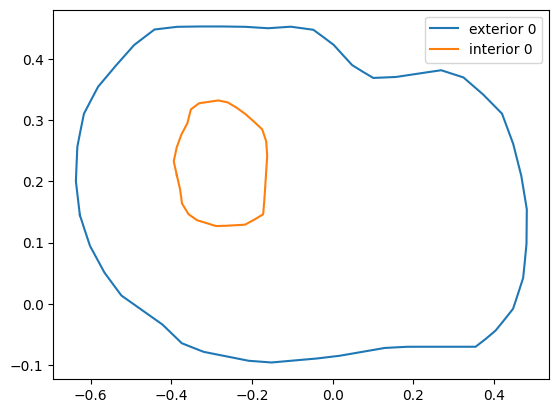
bnd = g.boundary_polygons
ext0 = bnd.exteriors[0]
plt.plot(ext0.xy[:,0], ext0.xy[:,1], label='exterior 0')
int0 = bnd.interiors[0]
plt.plot(int0.xy[:,0], int0.xy[:,1], label='interior 0')
plt.legend();

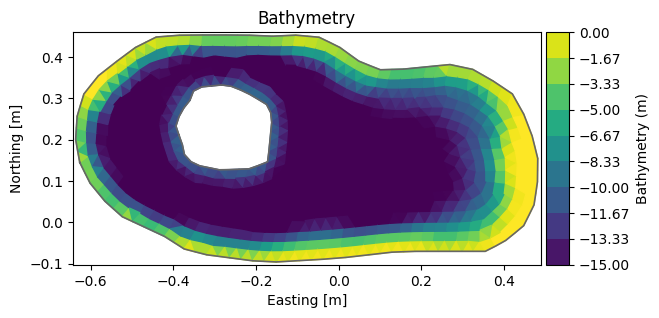
Change depth

# zn == nodes, not elements!
nc = g.node_coordinates
nc[:,2] = np.clip(nc[:,2], -15, 0) # clip depth to interval [-15,0]

Element coordinates are cached, delete to force recalculation

del g.element_coordinates

g.plot();

g.to_mesh('Fake_lake_clip15.mesh')   # save to a new file

See the MIKE IO Mesh Example notebook for more Mesh operations (including shapely operations).