Parameter identification

Parameter identification is about computing the optimal numerical value for each parameter in the network model, based on available measurement data. The parameters in the network model generally have a connection or interpretation of some physical effect, such as pressure loss induced by the friction between a pipe wall will and flowing water, or by elevation in the terrain.

While a parameter like elevation should be readily obtained from the asset management database, other parameters must be derived in an optimization program. As will be demonstrated in this section, a least squares program is a suitable optimization method. Using this method a relevant interval of measurement data should be selected, as a training dataset. In this project, 30 days was selected as a suitable duration of measured data, based on investigations into the seasonality of the water demand in weekly and annual timescales.

Least squares program

This is a least squares type program, with the general form:

$$\min\limits_{x} f(x)= \frac{1}{2} || A x - b ||_2^2$$

The optimal solution, $x^*$, for a least squares problem is:

$$x^* = (A^T A)^{-1} (A^T b)$$

The application in this project has the parameters in the $x$ vector and the measurement data in the $A$ matrix and $b$ vector respectively. It is important to realise the following about the linear properties for the least squares program compared to other methods used in this project: There is a requirement that the matrix form is linear with respect to $x$, ie. the form $Ax - b = 0$. However, as will be shown in the next section, with this method, flow and pressure are prior known. Therefore, non linear operations can be applied to the measurements, prior to solving the program.

Pipe resistance identification

Pipe resistance utilises a simplified version of the network model, taking resistance parameters as states and measurements as boundary conditions. For each pipe as a standalone unit, it has the formula:

$$\Delta H = \alpha |q|q$$

In a least squares form, it takes the following form:

$$\min\limits_{\alpha > 0} f(\alpha)= \frac{1}{2} || |q|q \alpha - \Delta h ||_2^2$$

where $\Delta h$ and $q$ are vectors in time and $\alpha$ is a scalar. Note, that we can use the squared flow in the program, as discussed in the section above. Therefore, it is possible to use the network model in non-linearised form, unlike in the control program, where the flow constitute a state, rather than a boundary.

This program has the optimal solution:

$$\alpha^*=(|q| q^T |q|q)^{-1} (|q| q^T \Delta h)$$

For a system with multiple pipes the equation is extended as follows, where the transposed incidence matrix $Ic^T$ is introduced.

$$Ic^T*h= |q|q*I*\alpha$$

$$Ic^T = \begin{bmatrix} 1 & -1 & & \\ & 1 & -1 & \\ & 1 & & -1 \\ & & 1 & -1 \end{bmatrix}$$

$Ic^T*h$ gives the pressure differences for the system in one timestep. $|q|q*I*\alpha$ is another form, giving pressure differences in one timestep, which is equivalent to multiplying the vectors by elements.

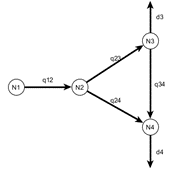
The ‘long form’ is used to extend the problem to any length of timesteps. In the example below two steps is shown:

$$\begin{bmatrix} Ic^T & \\ & Ic^T \end{bmatrix} * \begin{bmatrix} h_{1,1} \\ h_{2,1} \\ h_{3,1} \\ h_{4,1} \\ h_{1,2} \\ h_{2,2} \\ h_{3,2} \\ h_{4,2} \end{bmatrix} = \begin{bmatrix} (|q|q)_{12,1} & & & \\ & (|q|q)_{23,1} & & \\ & & (|q|q)_{24,1} & \\ & & & (|q|q)_{34,1} \\ (|q|q)_{12,2} & & & \\ & (|q|q)_{23,2} & & \\ & & (|q|q)_{24,2} & \\ & & & (|q|q)_{34,2} \end{bmatrix} \begin{bmatrix} \alpha_{12} \\ \alpha_{23} \\ \alpha_{24} \\ \alpha_{34} \end{bmatrix}$$

where: $$ I^{2x2} \otimes Ic^T = \begin{bmatrix} Ic^T & \ & Ic^T \end{bmatrix}$$ is the kronecker product. $I^{n x n}$, the size of the identity, is equivalent to the $n$ timesteps or samples from the system. The matrix of flow samples is given by stacking block matrices in the form $(|q|q)_n I$ for each $n = 1 .. N$ timesteps or samples.

Pump parameter identification

Pump discharge and pressure are linked properties. This is the system characteristics related to the pump, which determines the work that the pump exerts on the water.

This is the system characteristics for the pump, represented in a first order function:

$$p = aq + b$$

The model parameters are identified in the same way as described by pipe resistance identification. This has semblance with the linearised network model, but is not the same. The difference is conceptual. The pump model represents not a section of pipe, with a physical length representation, but a singular point which induces flow and pressure unto the network. The most important reason that this model is linear with respect to flow, $q$, is, so it can be embedded in the control program.